yarım saattir uğraşıyorum bu soruyu çözemedim?

  • Konbuyu başlatan Konbuyu başlatan kaybil
  • Başlangıç tarihi Başlangıç tarihi
Kodla Büyü
gunica' Alıntı:
@eynelmefer hocam bu sayıları hesaplayarak mı buldunuz yoksa çizerek mi? sonuçta sınavda olsa çizmenin mümkünatı yok sonuçta.. hesaplamasını da anlatır mısınız?
Genişletmek için tıkla ...

hocam,
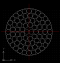
çapa (ekvatora) 10 tane konuyor bunda sanırım hem fikiriz
sonra güney kutbuna doğru iniyoruz yavaş yavaş,
çaptaki çemberler 1 cm güneye 1 cm kuzeye olacak şekilde tam ortalı yerleşiyor, ve ekvatordan 1 cm uzaktaki paralel ikinci sırayı yerleştiriyoruz bu da en fazla tam sayı olarak 9 olur, zaten 10 olsa dikdörtgen olması gerekirdi ama kıvrımlar başladığı için 10 tane sığmayacaktır en fazlayı istediği için 9 tane yerleştiriyoruz, bu şekilde ikinci sırayı da yerleştirdikten sonra 3. sıraya geçiyoruz, mantık aynı bu sefer 9 tane sığmayacağı için 8 tane yerleştiriyoruz, bu arada ekvatordan 5 cm uzaklaşmış oldu 3. sıranın çemberinin en uzak noktası, 4. sırada 7 tane ve son olarak nihayet 5.sıraya geldiğimizde 6 tane yerleştiriyoruz bunun aynısını kuzey kutbu içinde yaparsak:
10+9+8+7+6+9+8+7+6=70 cevabını buluruz, anlatamadıysam son olarak şekil çizerim ama amaç hasıl olmuştur diyerek, cevabımı söylemiş olayım :)

90 diyen arkadaşlar içinde, şöyle bi not düşeyim:
4tane daireyi bir karenin içine yerleştirdiğinizde 4 cm^2 boşluk kalıyor (çemberlerin yarıçapı 1 yine, karenin bir kenarı 4 oluyor)
3tane daireyi bir üçgenin içine yerleştirdiğimizde yaklaşık 2,6 cm^2 boşluk kalıyor (çemberlerin yarıçapı 1 yine, üçgen eşkenar üçgen)
90 tane daireyi yerleştirdiğinizde sadece 10 cm^2 boş alan kalması da baya baya zor olsa gerek diye düşündüm...

öyle işte:)
 
Yap bi program, döndür for döngüsünün içinde. Bulsun.
 
Daire şeklinde olunca olmuyomuş, 79 tane sığdırabildim :mrgreen:

Eynelmefer hocam o söylediğiniz yönteme göre dairelerin tam üst üste gelmesi lazım. Öyle olmadan iki dairenin ortasından devam edecek şekilde dizince daha az boşluk kalır. Yani en basitinden bilardo toplarının dizilişini düşünün. 5 sırayı bilardodaki gibi dizince üçgen olur evet ama çapları toplamı 10 cm değil 4 kök 3 +2 cm gibi bi değer olur. Dolayısıyla yukarda en az bi tane daha sığacak kadar yer kalıyor. Cevap matematiksel olarak da kesinlikle 70'ten büyük.
 
iç içe halkalar şeklinde en dıştan yerleştirmeye başlarsak daha çok yerleşir sanki...
toplamda sosislerden oluşan 5 tane halka olabilir. sosislerin çapı 2cm.
en dışa halka 9 cm yarıçaplı olur onun da çevresini hesaplayıp yerleştirirsek 27 tane ilk halkada
sonraki halka 7 cm yarıçaplı olur onun da çevresini hesaplayıp yerleştirirsek 21 tane bu halkada
sonraki halka 5 cm yarıçaplı olur onun da çevresini hesaplayıp yerleştirirsek 15 tane bu halkada
sonraki halka 3 cm yarıçaplı olur onun da çevresini hesaplayıp yerleştirirsek 9 tane bu halkada
en iç sosis halkası da 1 cm yarıçaplı olur oraya da 3 tane (? bundan tam emin olamadım)
toplamda 27+21+15+9+3 = 75
 
benim pizza da en fazla 30 tane çıktı
 

Ekli dosyalar

  • sucuklupizza.jpg
    sucuklupizza.jpg
    97.8 KB · Görüntüleme: 384
AutoCAD en fazla bu diyo ama saymadım üşendim merak eden saysın :)
 

Ekli dosyalar

  • Adsız.png
    Adsız.png
    19.4 KB · Görüntüleme: 366
bu soru formülle filan değil atmasyon çözülecek bi soru bence :) yaklaşık olarak 70 olur :)
 
Bugün bizim matematik öğretmenine sordum.15 dakika uğraştıktan sonra kareli bir defter sayfasına çizerek 70 sonucunu buldu.Sonuç yetmiş miş miş miş....
 
SOru türev sorusu, şu kadar alana en fazla ne kadar tarzı sorular türev sorusudur, ama nasıl çözülür unuttuk türevi mürevi, matematikçilerin çözmesi lazım iki dakkada aslında. Ama ilköğretim matematikçiler değil - branşçılar.
 
2010 yılında Van hie den web tabanlı içerik geliştirme kursundan gelirken yolda çay içelim diye durdum. elime aldığım kesme şekerleri bilye ,bardağı da silindir olarak düşündüm acaba bunu bardak ve şekerin animasyonu yapsam kaç adet sığacağını bulabilir miyim diye düşündüm muhabbet olsun diye diğer eğitici arkadaşa sordum "silindire sığan bilye sayısını " bulursan çaylar benden dedim . etraflıca düşünmeyince kolay gibi gelmiştir.ama sonra anladık ki rakamlar işi çok zorluyor. olayı flashtan kurtardık algoritması üzerinde kafa yorduk ama nafile problem gerçekten büyüktü.Sonra problemi şu şekilde sormaya başladım etrafımdakilere.
"yarıçapı r olan bir silindir kabın içine yarıçapı p olan kaç bilye sığar. Bunun bir ambalaj fabrikasında yaşanmış sorun olarak anlatıyorum :) "

Bir iki ay sonra Rize hie de matematik öğretmenlerine kursa gidince orada matematikçilere sordum. çok düşündüler yazdılar çizdiler olmadı. Bir hocamız Amerika da yüksek lisans yapan arkadaşına sormaya gitti bir gün sonra yanımıza geldi Amerika dan gelen cevap bizi şaşırttı.
Arkadaşın gönderdiği cevaba göre net sonucu veren bir formül yokmuş. sadece yaklaşık değeri veren birtakım deneylerden sonra elde edilen grafiklerin formülleri varmış falan filan. Konjonktürel çözümleri varmış . nedemekse bu :D
Sonuçta problem ortada kaldı.
 
Cevap yazmak için giriş yap yada kayıt ol.
Geri
Üst